Multiphysics made easy with random coloured graphs
31 January 2019
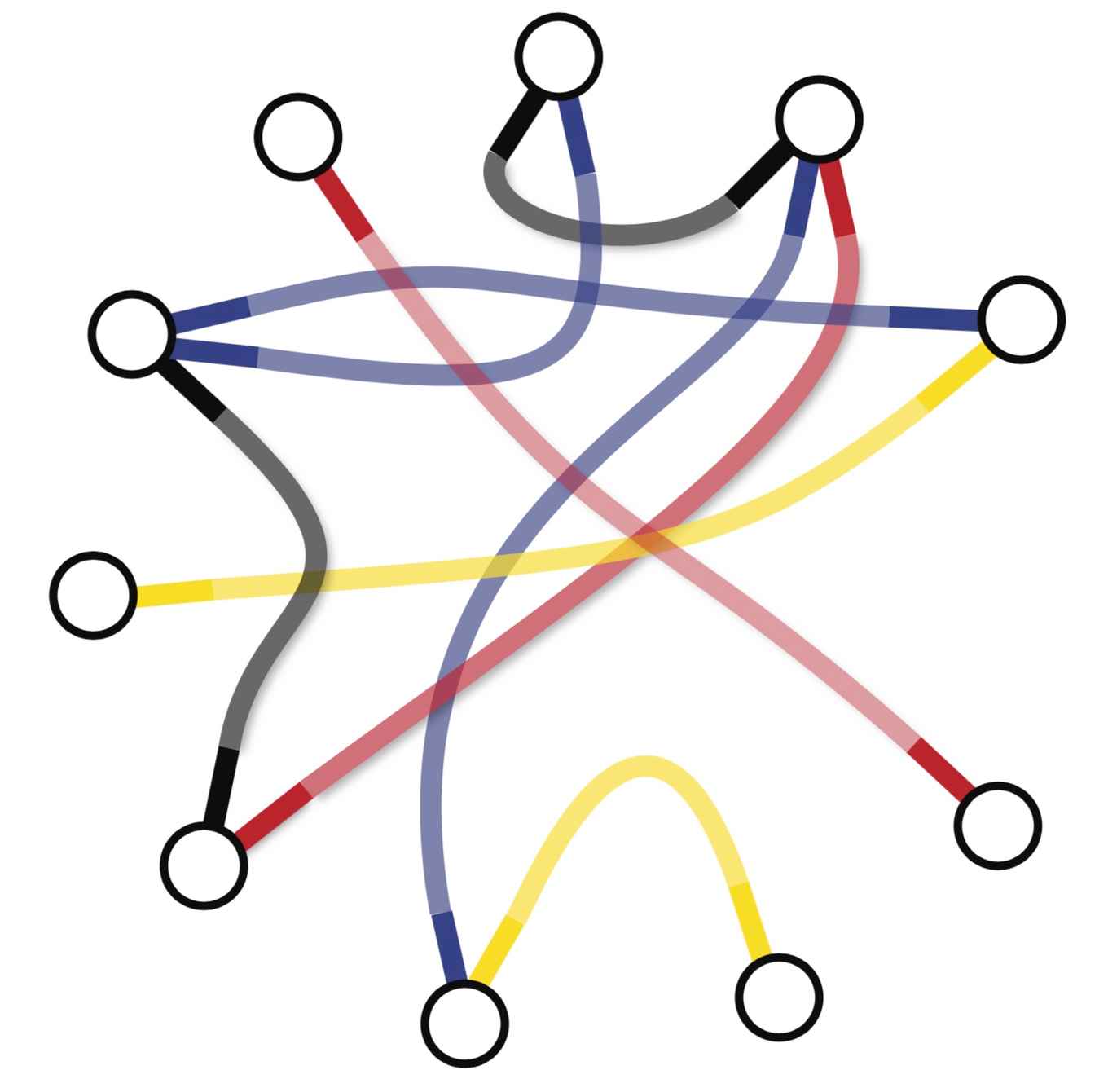
The utterly familiar way to represent chemical compounds by diagrams of dots connected by dashes - a 'molecular graph' - appeared in the early 18th century. Around that time, Isaac Newton's notion of gravity had led to speculative ideas that atoms are held together by a kind of ‘gravitational force’. These ideas gradually evolved: in 1758 Scottish chemist William Cullen used in his lectures what he called ‘affinity diagrams’ to represent forces supposedly existing between pairs of reactive molecules. Twenty years later, William Higgins used similar diagrams in his book to represent forces within molecules.
These events were happening in parallel with a series of dramatic discoveries in contemporary mathematics. It started in 1736 with Leonard Euler desperately trying to sketch a route though seven bridges of Königsberg in such a way that each bridge is crossed only once. Euler proved that such a route does not exist by using very similar diagrams to ‘affinity diagrams’ of Cullen and Higgins. The theory that Euler laid out in his proof is now an independent discipline called graph theory.
Graph theory has become instrumental for detecting when two molecules are said to be identical, defining functional groups and isomers. It provides the basis for synthesis and molecular mining. In short, graph theory is the language of modern chemistry.
When randomness meets rigour
Despite tremendous success, the concept of a molecular graph has a detrimental flaw hidden deeply at its core: as a means to represent well-defined structures, the molecular graph spares no place for randomness. In crystallography this problem did not surface since the places where the real world structures deviate from the template were simply called 'defects'. When matter is amorphous, however, the whole structure consists of such defects and there's little to no sense to talk about any rigid template then.
The state-of-the-art idea that provides the way out of this riddle is the concept of the random graph. This allows combining the 'fluidity' of the structure with the possibility of rigorous description. However, implementing different types of connections in a random graph, representing different types of interactions, has been an open problem for quite some time. Such interaction may denote physical forces of different nature, different combinations of interacting agents, interactions happening in different conditions, and other crucial factors that together are known as 'multiphysics'.
Multiphysics made easy
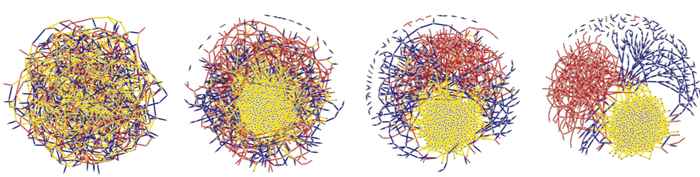
Thus, in order to render random graphs palatable for the real, physical world, it is important to be able to differentiate between different types of connections. The recent publication of Ivan Kryven in Nature Communications does exactly that. Kryven introduces a theory that links the local statistical description of a random graph to its emergent global properties. The theory allows many interactions, exemplified by colours, to coexist in random graph modelling. Thanks to this property, the model may capture the interplay of many physical factors.
Just as graph theory is the alphabet of modern chemistry, coloured random graphs have a potential of becoming the new lingua franca of the physics and chemistry of disordered matter. It also turns out that multiple colours may point the way to observing new types of behaviour that have not been observed before. For instance, multiple phase transitions or macroscopically observable fluctuations may emerge in reactive systems. Trilled by these new theoretical discoveries, the Computational Polymer Chemistry Group led by Prof. Pieter Iedema is setting off for the search for physical systems that feature these peculiar phenomena.
The research described above has been performed as part of the research programme VENI financed by the Netherlands Organisation for Scientific Research (NWO).
Publication details
I.Kryven ”Bond percolation in coloured and multiplex networks”, Nature Communications 10, 404. DOI: 10.1038/s41467-018-08009-9