And the secret ingredient is… the network
Advances in polymer materials engineering through mathematical network analysis
25 February 2019
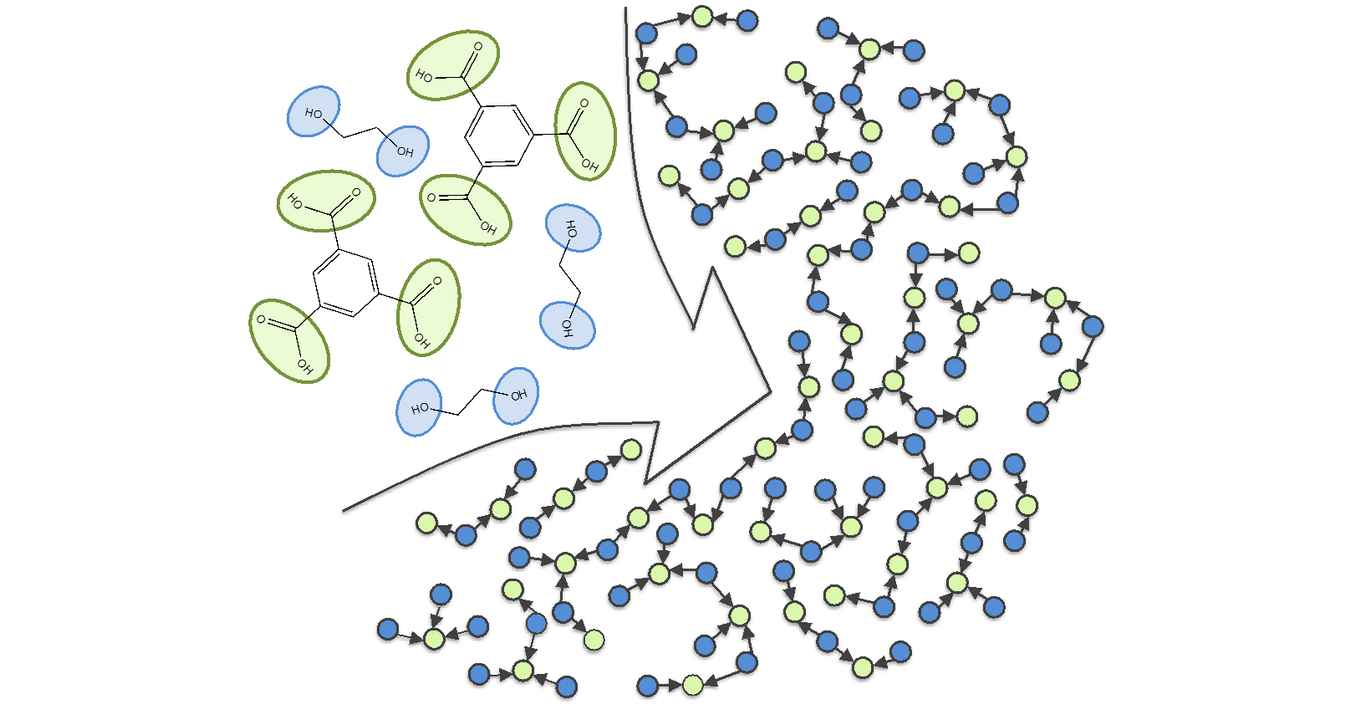
Polymers are huge molecules built from thousands or even millions of copies of a small 'monomer' molecule. These are chemically strung together in a chain-like fashion, or - provided they are able to link to each other in three or more ways - form a complex molecular network. This process of polymerisation is used to manufacture a broad range of materials, from plastic bottles to composite dental fillings. But the binding medium in old masters’ paintings also consists of polymers.
Materials researchers striving to obtain durability of plastics or prevent degradation of oil paintings often struggle with the complex molecular characteristics of polymers. In many cases the only viable approach is that of trial-and-error, for instance in producing, testing and discarding samples until finally the right polymers and polymerisation conditions are obtained.
Mathematical network analysis
Now, PhD student Verena Schamboeck and supervisors Piet Iedema and Ivan Kryven from the University of Amsterdam's Van 't Hoff Institute for Molecular Sciences present a polymerisation model based on mathematical network analysis that can significantly speed up this process and helps to save money and environmental resources. The model has just been published in Nature Research's open access journal Scientific Reports.
The Amsterdam researchers focus on the process of so-called step-growth polymerisation, where multifunctional monomers react in a step-by-step manner to form big polymer networks. Many naturally occurring and synthetic polymers are produced by such step-growth polymerisation.
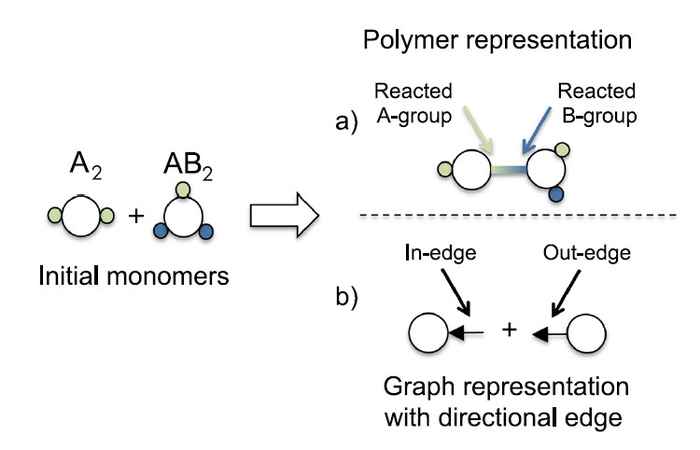
Schamboeck and co-workers describe the structure of the polymer network by means of mathematical graph theory. The monomers are identified as the nodes in the graph network and the connections between these nodes represent the molecular bonds between the monomers. As monomers may carry different types of reactive parts these connections might be asymmetric. Hence arrows are used to distinguish the two different sides of the connection.
In this way, the researchers obtain new analytical expressions describing the polymeric microstructure. Using state-of-the art mathematical theory they investigate the properties of the multiplex networks and compare these to data from experiments and computer simulations. They thus are able to link the results of the network analysis to the mechanical properties of the polymer. For example, their analysis predicts the transition from a liquid to a solid during the formation of the polymer. They show that this transition corresponds to a phenomenon in network theory called percolation. Furthermore, they were able to predict relevant parameters such as the molecular weight distribution and molecular gyration radii.
Schamboeck and coworkers thus show that once the structural basics of a polymer network are known, a network analysis can assist in a more effective design of new materials and optimisation of their properties.
Publication details
Schamboeck, Verena, Iedema, Piet D. and Kryven, Ivan ”Dynamic Networks that Drive the Process of Irreversible Step-Growth Polymerization”, Scientific Reports (2019). DOI: 10.1038/s41598-018-37942-4